Newman投影式によるブタンの立体配座 96回薬剤師国家試験問5
第96回薬剤師国家試験 問5
Newman投影式 I〜Ⅵは、ブタンの立体配座を表したものである。
下記の記述a〜eの正誤を判定してみよう。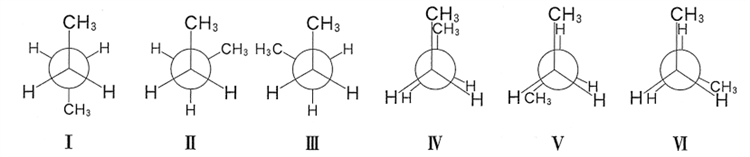
a I〜Ⅲは「重なり形配座」、Ⅳ〜Ⅵは「ねじれ形配座」とよばれる。
b Iは「アンチ形」、Ⅱ及びⅢは「ゴーシュ形」とよばれる。
c I〜Ⅵの中で最も安定な立体配座は、Iである。
d Ⅱ及びⅢは、同じ安定性を示す。
e I〜Ⅵの中で最も不安定な立体配座は、V及びⅥである。
第96回薬剤師国家試験 問5 解答解説
◆ aについて
a × I〜Ⅲは「重なり形配座」、Ⅳ〜Ⅵは「ねじれ形配座」とよばれる。
→ ○ I〜Ⅲは「ねじれ形配座」、Ⅳ〜Ⅵは「重なり形配座」とよばれる。
結合同士が重なる立体配座を重なり形配座といい、各結合同士の二面角が60°となる立体配座をねじれ形配座という。

よって、下記の通り、Ⅰ〜Ⅲはねじれ形配座であり、Ⅳ〜Ⅵは重なり形配座であり。

Ⅳ〜Ⅵの「重なり形配座」では、結合同士が重なることで生じる電子雲同士の反発によるねじれひずみ(二面角ひずみ)がある。
一方、I〜Ⅲの「ねじれ形配座」は結合同士の重なりは無いため、ねじれひずみは無い。
よって、I〜Ⅲの「ねじれ形配座」はⅣ〜Ⅵの「重なり形配座」よりもエネルギーが低く、安定である。
◆ bについて
b ○ Iは「アンチ形」、Ⅱ及びⅢは「ゴーシュ形」とよばれる。

Ⅰのように、2つのCーCH3結合の二面角が180°で、2つのメチル基が最も離れる配座は、ねじれ形配座の中でもアンチ形と呼ばれる。
ねじれ形のアンチ形は、最も安定な配座である。

ⅡおよびⅢのように、2つのC−CH3結合の二面角が60°の配座は、ねじれ形配座の中でもゴーシュ形と呼ばれる。ゴーシュ形では、2つのメチル基が近接することによる立体ひずみが生じるので、ねじれ形に比べてエネルギーは高い。
◆ c・d・eについて
c 〇 I〜Ⅵの中で最も安定な立体配座は、Iである。

d 〇 Ⅱ及びⅢは、同じ安定性を示す。
ⅡとⅢはどちらもゴーシュ形配座であり、ポテンシャルエネルギーが同じなため、同じ安定性を示す。

e × I〜Ⅵの中で最も不安定な立体配座は、V及びⅥである。
→ 〇 I〜Ⅵの中で最も不安定な立体配座はⅣである。

Ⅳの配座は、結合同士が重なることによるねじれひずみに加え、2つのメチル基が近接することによる立体ひずみが生じるため、
ブタンで最も不安定な立体配座である。
以下、詳細
ブタンの各立体配座の安定性を考える際は、
次の①と②のひずみの有無がポイントとなる。
① 結合同士が重なることで生じる電子雲同士の反発によるねじれひずみ(二面角ひずみ)
② メチル基同士が近接することで生じるファンデルワールス反発力による立体ひずみ
これらのひずみがあると、その分エネルギーは高くなり、安定性は低くなる。
◆ Ⅰについて

Ⅰはねじれ形なので、結合同士が重なることによるねじれひずみは無い。
さらに、2つのメチル基が互いに180°で最も離れているので、メチル基同士の立体ひずみはない。
よって、Ⅰは最もエネルギーの低い、最も安定な立体配座である。
◆ ⅡおよびⅢについて

ⅡおよびⅢはねじれ形なので、結合同士が重なることによるねじれひずみは無い。
しかし、2つのメチル基が互いに60°で、メチル基同士のファンデルワールス反発力による立体ひずみが生じる。
よって、ⅡおよびⅢのゴーシュ形は、Ⅰのアンチ形に比べてエネルギーは高い。
◆ Ⅳについて

Ⅳは重なり形で、結合同士が重なることによるねじれひずみがある。
さらに、2つのメチル基が近接するため、メチル基同士のファンデルワールス反発力による立体ひずみが生じる。
よって、Ⅳは最もエネルギーの高い、最も不安定な配座である。
◆ ⅤおよびⅥについて

ⅤおよびⅥは重なり形で、結合同士が重なることによるねじれひずみがある。
2つのメチル基が離れているため、メチル基同士の立体ひずみは生じない。
よって、ⅤおよびⅥは、Ⅳに比べるとエネルギーは低い。
下の図は、ブタンのC2−C3の結合の回転による配座の変遷とポテンシャルエネルギーの変化を表す。

★参考外部サイトリンク
立体配座(wikipediaさん)