弱酸性薬物のpH5からpH8における溶解した非解離形薬物濃度を示すグラフはどれか 94回薬剤師国家試験問169
第94回薬剤師国家試験 問169
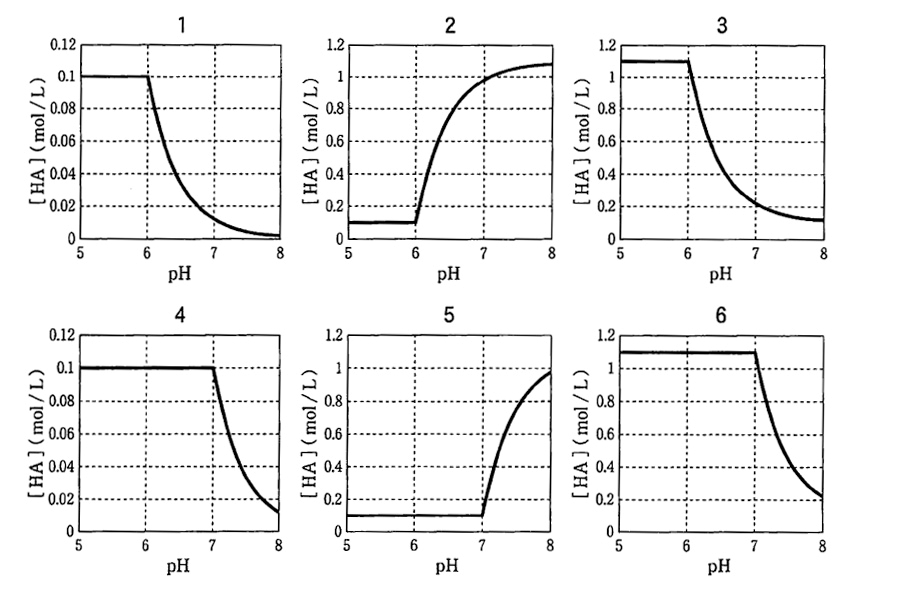
弱酸性薬物は水溶液中で
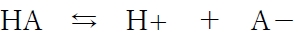
のように解離する。
pKa値が5.0、非解離形薬物HAの溶解度が0.1 mol/Lである弱酸性藥物の結晶0.11 molを0.01 mol/Lの塩酸0.1 Lに懸濁し、塩基Bを少量ずつ添加していくとき、pH5からpH8における溶解した非解離形薬物濃度 [HA] を示すグラフは次のどれか。ただし、HA及びA−は塩酸及び塩基Bと反応せず、結晶の溶解及び塩基Bの添加による体積変化は無視できるものとする。
第94回薬剤師国家試験 問169 解答解説
正解は1である。
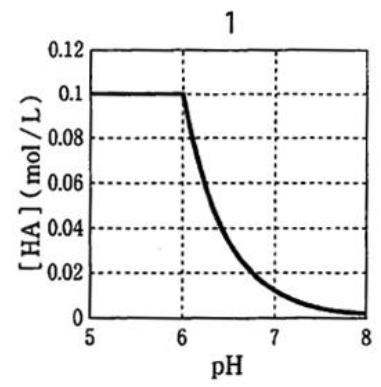
本問の弱酸性薬物の溶液は、pHが低い時には溶けきれない薬物の固相が存在している飽和溶液であり、pHが上がるにつれて弱酸性薬物の溶解度が上昇していき、どこかのpHで固相が消失する。そのpHを境に飽和溶液ではなくなる。pHがさらに上昇すると、分子形の濃度は低下し、イオン形の濃度は上昇する。
本問では、1価の弱酸性薬物における、
”pHの変化に対する分子形・イオン形の存在比の変化”
および
”pHの変化に対する溶解度の変化”
についての理解が必要である。
弱酸性物質におけるpHの変化に対する分子形・イオン形の存在比の変化の解説 へ
問題文の「非解離形薬物HAの溶解度が0.1 mol/Lである」という記述から、
この弱酸性薬物の飽和溶液における分子形濃度([HA]飽)は0.1 mol/Lだとわかる。
次に、「弱酸性藥物の結晶0.11 molを0.01 mol/Lの塩酸0.1 Lに懸濁し」という記述より、
この初期の状況において溶液はどのような状態なのかを考えてみる。
0.01 mol/Lの塩酸のpHを計算すると、
塩化水素HClは水中で、
HCl → H+ + Cl−
の形に完全に電離すると仮定すると
0.01 mol/Lの塩酸の水素イオン濃度は0.01mol/Lなので、
pH=−log[H+]より、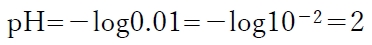
ここで、溶液におけるある物質の“含有量”を便宜的に下記のように定める。
ある物質の含有量=(溶解していない物質量+溶解している物質量)/溶媒の量
「弱酸性藥物の結晶0.11 molを塩酸0.1 Lに懸濁した」とあるが、溶液中の弱酸性薬物の含有量を計算すると、0.11mol/0.1L=1.1mol/L
溶液中で溶解平衡が常に成立するとすると、
あるpHにおいて溶液が飽和溶液か飽和溶液でないかの判断は下記のように行える。
そのpHにおける溶解度≦含有量 ならば飽和溶液である。
そのpHにおける溶解度>含有量 ならば飽和溶液でない。

ゆえに、pH=2では、
pH2の時の溶解度(0.1 mol/L)≦含有量(1.1mol/L)
であり、溶解度以上に物質が含有されているため、
飽和溶液である。
よって、pH=2の時の分子形濃度は[HA]飽の0.1 mol/Lである。
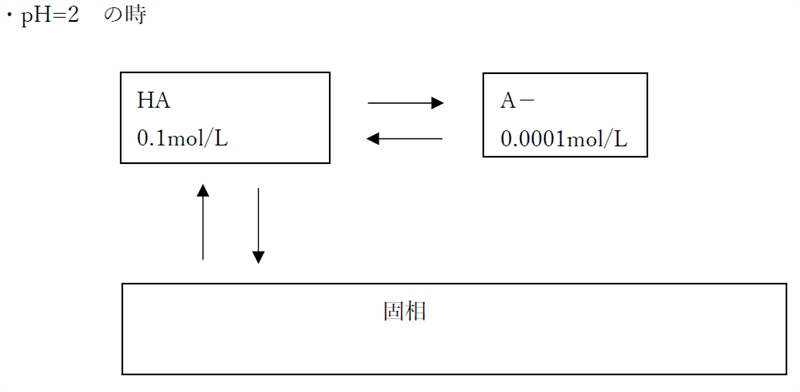
以下では、pH=5〜8における分子形濃度について考える。

1価の弱電解質ではpH=pKaの時に分子形とイオン形の濃度が等しくなる。
よって、1価の弱電解質の溶解度について、pH=pKaの時の溶解度は2×[HA]飽に等しい。
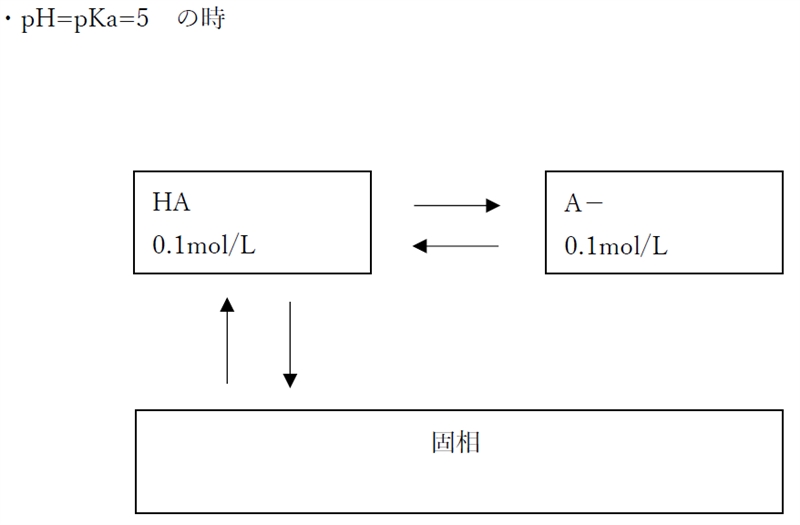
ゆえに、pH=5では、
pH5の時の溶解度(0.2mol/L)≦含有量(1.1mol/L)
であり、溶解度以上に物質が含有されているため、
飽和溶液である。
よって、pH=5の時の分子形濃度は[HA]飽の0.1 mol/Lである。
なお、pH=5の時のイオン形濃度も0.1 mol/Lである。

ゆえに、pH=6では、
pH6の時の溶解度(1.1mol/L)=含有量(1.1mol/L)
であり、溶解度と等しい量の物質が含有されているため飽和溶液である。
よって、pH=6の時の分子形濃度は[HA]飽の0.1 mol/Lである。
なお、pH=6の時のイオン形濃度は1.0 mol/Lである。
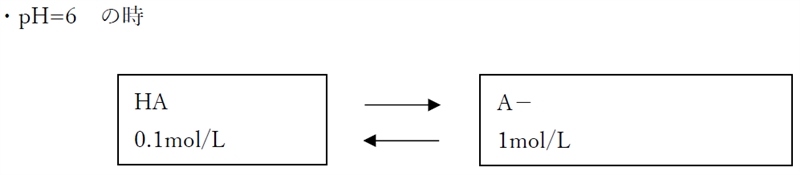
pH=6では、溶解度=含有量なので、飽和溶液であるが固相は消失している。
よって、pHが6より大きい値では、
溶解度>含有量 となるので、
飽和溶液ではなくなる。
飽和溶液である間は、pHが上昇して溶解度が上昇しても、固相からHAは溶け出すことで、分子形HAの濃度は[HA]飽で一定の値に保たれていた。
飽和溶液でなくなると、pHが上昇して分子形から陰イオン形へ変わるものが増えるに伴い、分子形濃度は低下することになる。

ゆえに、pH=7では、
pH7の時の溶解度(10.1mol/L)> 含有量(1.1mol/L)
であり、飽和溶液ではない。
pH=7の時の分子形濃度を求めてみる。
弱酸性物質のヘンダーソン・ハッセルバルヒの式として次式が成り立つ。
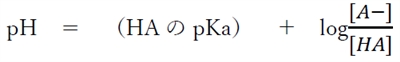
この式を元にして、あるpHにおける分子形とイオン形の存在比(存在割合)が求まる。
式を変形して、
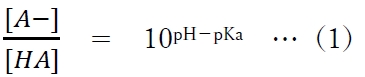
(1)式にpH=7.0,pKa=5.0を代入すると
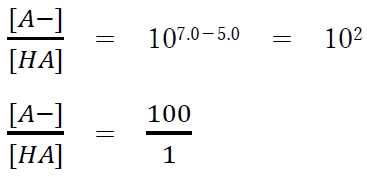
よって、pH=7.0では、
分子形:イオン形=1:100 の存在比である。
ゆえに、
pH=7における分子形濃度は次のように計算できる。
pH7における分子形濃度 = 全濃度×(pH7での分子形の比率)

なお、pH7でのイオン形濃度は、
pH7におけるイオン形濃度 = 全濃度×(pH7でのイオン形の比率)
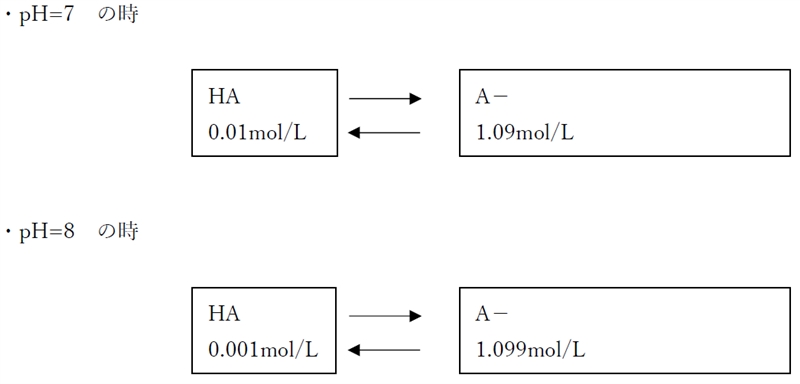
以上より、正解は1のグラフである。
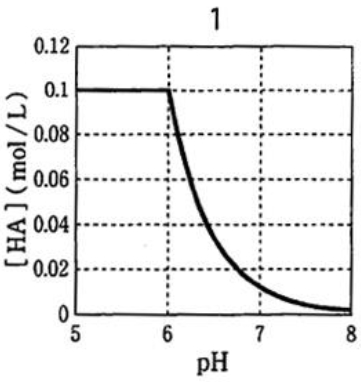
★参考外部サイトリンク
pHおよび解離定数(yakugaku labさん)