不斉炭素の数と立体異性体の数の例外 82回薬剤師国家試験問8d
第82回薬剤師国家試験 問8d
下記のCに関する記述の正誤を判定してみよう。
が存在する.jpg)
d Cには4個の不斉炭素(キラル中心)が存在する。
第82回薬剤師国家試験 問8d 解答解説
d ○ Cには4個の不斉炭素(キラル中心)が存在する。

Cには4個のキラル中心が存在するが、立体異性体(光学異性体)の数は8個しかないことも併せて押さえておこう。
基本的に、ある化合物に不斉中心がn個あるとすると、その化合物を含め互いに立体異性体であるものの数は、各不斉炭素についてR,Sの二通りの立体があることから全部で(2のn乗)個あるはずである。
ただし、例外的に、不斉中心の数がn個でも、立体異性体の数が(2のn乗)個とならないこととして、次の(1)と(2)のことが挙げられる。
(1)立体異性体の中に分子内対称面のあるものが含まれる
(2)橋頭位が両方とも不斉中心である
本問の化合物Cは(2)が当てはまる。
環に橋がかかったような構造があり、橋のたもと(橋頭位)の原子が両方とも不斉中心という構造が1つあるごとに、立体配置異性体の数が半分になる。これは、橋構造が作れるように、2つの橋頭位の絶対配置の組み合わせに制約ができるためである(橋構造を作れない橋頭位の絶対配置の組み合わせがある)。
不斉中心の数がn個で、橋頭位の原子が両方とも不斉中心という構造がm個あるとすると、
その化合物の立体配置異性体の数は(n−m)の2乗個となる。
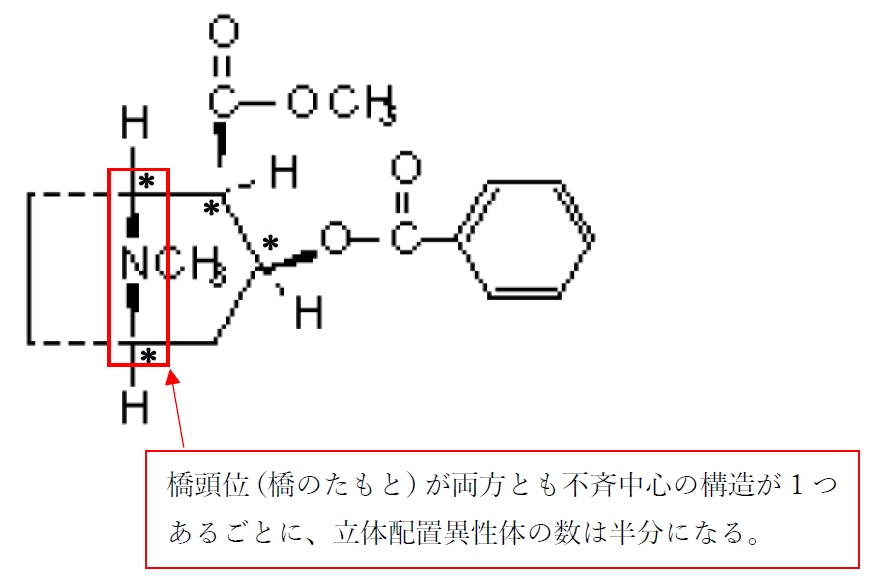
Cでは、不斉中心は4個で、分子内対称面はないが、橋頭位が両方とも不斉中心の構造が1つあるので、
立体異性体の数は(2の[4−1])乗個=(2の3乗)個=8個である。