薬剤師国家試験問題集 反応速度論

88回薬剤師国家試験　問23
3種類の薬物A、B及びCの分解は、それぞれ0次、1次及び2次反応に従う。次の記述のうち、正しいものはどれか。
a　Aの残存量は、時間と共に直線的に減少する。
b　Bの残存量の対数は、時間と共に直線的に減少する。
c　Cの残存量の逆数の対数は、時間と共に直線的に増加する。
d　いずれの薬物も、その初濃度と半減期が同じ場合、半減期以降での薬物の分解量の最も少ないのはAである。

トップページへ

 

薬剤師国家試験過去問題　科目別まとめ一覧　へ

 

薬剤師国家試験過去問題集　反応速度論　一覧へ

 

 

88回薬剤師国家試験　問23　解答解説

 

◆　aについて
a　〇　Aの残存量は、時間と共に直線的に減少する。

 

薬物Aの分解は0次反応に従う。
0次反応の特徴は下記のリンク先を参照
0次反応とは　速度式，半減期，グラフ

 

分解が0次反応に従う薬物の濃度（または含量）と時間の関係式として、
次式が成り立つ。

 

C = C₀ − k₀・ｔ　…�@
C：時間tでの反応物の濃度(含量)　C ₀：初期の反応物の濃度(初期含量)
k₀：0次反応速度定数

 

�@式より、反応が0次反応に従う場合、
時間に対して反応物の濃度(含量)をプロットすると、
傾きが−k₀の右下がりの直線が得られる。

 

 

 

◆　bについて
b　〇　Bの残存量の対数は、時間と共に直線的に減少する。

 

薬物Bの分解は1次反応に従う。
1次反応の特徴は下記のリンク先を参照
1次反応とは　速度式，半減期，グラフ

 

分解が1次反応に従う薬物の濃度（または含量）の自然対数と時間の関係式として、
次式が成り立つ。

 

lnC = lnC₀ − k₁・ｔ　…�A
C：時間tでの反応物の濃度(含量)　C₀：反応物の初濃度（初期含量）
k₁：一次反応速度定数　t：時間

 

�A式より、分解が一次反応に従う場合、
時間tに対して反応物の濃度の自然対数(lnC)をプロットすると、
傾きが−k ₁の右下がりの直線が得られる。

 

 

また、
�A式に lnC = 2.303 log₁₀C を代入すると、
時間と濃度の常用対数の関係式として、
次の�B式が得られる。

 

 

 

◆　cについて
c　〇　Cの残存量の逆数の対数は、時間と共に直線的に増加する。

 

薬物Cの分解は2次反応に従う。
2次反応の特徴は下記のリンク先を参照
2次反応とは　速度式，半減期，グラフ

 

分解が2次反応に従う薬物の濃度(含量)の逆数と時間の関係式として、
次式が成り立つ。

 

 

 

◆　dについて
d　×　いずれの薬物も、その初濃度と半減期が同じ場合、半減期以降での薬物の分解量の最も少ないのはAである。

 

分解開始時の初濃度と半減期がA〜Cで同じ場合、
半減期以降での薬物の分解量について、
分解量の少ないものから、
C(2次反応)→ B(1次反応) → A(0次反応)
となる。

 

 

以下、詳細

 

0次、1次、2次の各反応の
半減期(t_1/2)の特徴は下記の通り。

 

・0次反応の半減期

 

上式より、0次反応の半減期は初濃度に比例する。

 

・1次反応の半減期

 

上式より、1次反応の半減期は初濃度に無関係で一定である。

 

・２次反応の半減期

 

上式より、2次反応の半減期は初濃度に反比例する。

 

以上のことから、
分解開始時の初濃度と半減期がA〜Cで同じ場合、
半減期以降での薬物の分解量について、
分解量の少ないものから、
C(2次反応)→ B(1次反応) → A(0次反応)
となる。

 

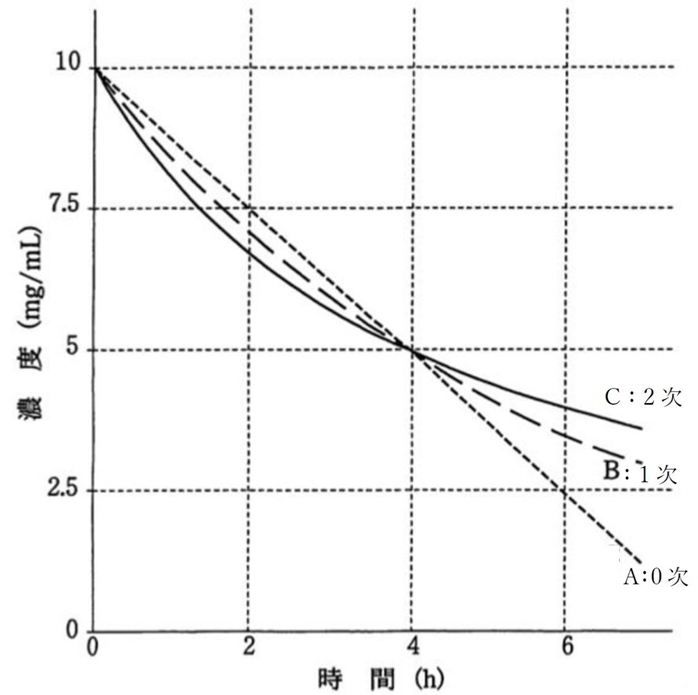
下の図はＡ〜Ｃについて、
分解開始時の初濃度が10mg/mL，半減期が4時間で等しい場合の
時間に対する濃度の推移を示したグラフである。

 

 

半減期以前では、
分解の反応速度は、速いものから、
C(2次反応)→ B(1次反応) → A(0次反応)
であり、
半減期以降では、
分解の反応速度は、速いものから、
A(0次反応)→ B(1次反応) → C(2次反応)
である。

トップページへ

 

薬剤師国家試験過去問題　科目別まとめ一覧　へ

 

薬剤師国家試験過去問題集　反応速度論　一覧へ